If you can make a classifier learn the difference between cats and dogs, you can make a classifier that distinguishes between pictures that are real and pictures that are generated.

Tôi không rõ ai là tác giả của câu nói này, có lẽ đó là một câu nói phổ thông mà bất kỳ ai cũng có thể nói ra, tôi xin mượn lại để bắt đầu một series vô cùng thú vị.

Nội dung bài viết

• Một cái nhìn tổng quan
  • GAN là gì ?
  • Các cột mốc (milestones) quan trọng (liên tục bổ sung)
• Đi sâu vào khám phá GAN
  • Minimax game
    • Minimax theo Von Neumman
  • Cách mà GAN hoạt động
    • Latent space
    • Kẻ lừa đảo (Generator) và Người cảnh sát (Discriminator)
  • Các hàm mất mát (loss function)
    • Định lý quan trọng nhất của bài báo (Định lý 1)
    • Thuật toán GAN
    • Mệnh đề về sự hội tụ trong GAN
  • Các hạn chế (Drawbacks) của GAN
• Tài liệu tham khảo

Thuật ngữ chuyên ngành

Thuật ngữ	Bản dịch tạm
Unsupervised Learning	Học không giám sát
GAN	Mạng chống đối tạo sinh
Generative model	Mô hình sinh
Generator	Bộ sinh
Discriminative model	Mô hình phân biệt
Discriminator	Bộ phân biệt
Latent space	Không gian ngầm ẩn
Encoder, Decoder	Bộ mã hóa, Bộ giải mã
Virtual training criterion	Mục tiêu huấn luyện ảo
Nash Equilibrium	Cân bằng Nash
Zeros-sum games	Trò chơi có tổng bằng 0

Một cái nhìn tổng quan

GAN là gì ?

Ian J. Goodfellow, một học trò xuất sắc của nhà sáng lập Coursera, Andrew Ng. Tài năng của anh thực sự bộc lộ qua giai đoạn làm tiến sĩ cùng với Yoshua Bengio, chủ nhân của giải thưởng ACM AM Turing 2018. Anh được biết đến rộng rãi trong cộng đồng AI nhờ ý tưởng thú vị nhất về Machine Learning trong vòng mười năm qua, Generative Adversarial Network, hay GAN.

Muốn nghe giảng về GAN từ chính cha đẻ của nó, xin mời bạn xem ở NIPS 2016 Workshop.

GAN dịch ra tiếng Việt là Mạng Chống Đối Tạo Sinh, là một thuật toán Unsupervised Learning được sinh ra với kỳ vọng tạo ra được những hệ thống có độ chính xác cao mà cần ít hoạt động của con người trong khâu huấn luyện.

Đây cơ bản là một mạng (network) được xây dựng bằng cách kết hợp nhiều mô hình trong Deep Learning, mà chút nữa ta sẽ đi sâu vào bàn luận. Sơ qua thì các mô hình này giống như Kakalot và Vegeta đánh nhau suốt cả đời vậy, khi trình độ của người này tăng lên thì người kia sẽ lại try hard để đấu tiếp, kết quả là sức mạnh của hai người không ngừng tăng lên, có thể nói họ là một cặp kỳ phùng địch thủ.

Chỉ khi sức mạnh của cả hai ngang cơ, họ mới thực sự thỏa mãn. Có thể nói theo một cách khác, xác suất thắng trong một trận đấu của họ khi đó là gần như nhau, xấp xỉ bằng \(\dfrac{1}{2}\).

Các cột mốc (milestones) quan trọng (liên tục bổ sung)

Phần này tôi chủ yếu dịch lại từ must read papers on gans. Do trình độ và thời gian nghiên cứu còn hạn chế, tôi chưa thể hiểu các bài báo này theo ý hiểu của riêng mình được. Tôi có dự định là sẽ tự đọc và note lại từng bài, cùng với đó là liên tục cập nhật các bài báo cải tiến mô hình hoặc phát minh ra những điều mới trong GANs.

1. GAN - Ian J. Goodfellow et al (2014)

   Bài báo bắt buộc phải đọc cho bất kỳ một ai muốn tìm hiểu về GANs. Bài báo này định nghĩa framwork của GAN và thảo luận về hàm mất mát non-saturating. Ngoài ra, bài báo cũng chứng tỏ hiệu quả của GAN bằng thực nghiệm trên các datasets ảnh như MNIST, TFD, CIFAR-10.

2. Conditional GANs — Mirza and Osindero (2014)

   Đây là một trong những chủ đề trung tâm của state of the art trong GANs. bài báo này cho thấy cách tích hợp class labels của các kết quả dữ liệu ổn định hơn trong quá trình training. Đây là một chủ đề được nhắc lại nhiều lần trong các công trình nghiên cứu về GAN trong các năm tiếp theo, đặc biệt quan trọng với những nghiên cứu mà tập trung vào image-to-image hoặc text-to-image.

3. DCGANs — Radford et al (2015)

   Bài báo này trình bày việc các lớp tích chập (convolution layers) có thể được sử dụng với GANs và cung cấp một loạt các hướng dẫn để thực hiện việc này. Bài báo cũng thảo luận về các chủ đề như Visualizing GAN Features, Latent Space Interpolation, sử dụng các tính năng của Discriminator để đào tạo phân loại và đánh giá kết quả.

4. Improved Techniques for Training GANs — Salimans et al (2016)

   Ian Goodfellow cũng là một trong những tác giả của bài báo này. Ở bài này cung cấp một chuỗi các gợi ý cho việc xây dựng kiến trúc mô hình dựa trên hướng dẫn đặt ra ở bài DCGAN. Bài báo này giúp hiểu được các giả thuyết về sự bất ổn trong GAN. Thêm vào đó, bài này còn cung cấp nhiều kỹ thuật bổ sung được thiết kế để giúp quá trình training của DCGANs được ổn định, bao gồm feature matching, minibatch discrimination, historical averaging, one-sided label smoothing, và virtual batch normalization

5. Pix2Pix — Isola et al (2016)

   Đây là một mô hình chuyển đổi image-to-image trong GAN. Framework này sử dụng các cặp training samples và nghiên cứu tinh chỉnh nhiều cấu hình trong GAN. Một trong những điều thú vị nhất trong bài báo này là việc thảo luận về PatchGAN: PatchGAN nhìn vào vùng \(70\times 70\) của bức ảnh để xác định ảnh đó là thật hay giả, so với cách thông thường là nhìn vào toàn bộ bức ảnh. Mô hình này còn cho thấy một kiến trúc thú vị: U-Net, cũng như là sử dụng các kết nối tắt (skip connections) kiểu Resnet trong Generator model. Có rất nhiều các ứng dụng hay, ví dụ như edge-maps to photo-realistic images: input là một bức ảnh chỉ có cạnh viền, output là ảnh thực hoàn chỉnh. Ví dụ với ảnh sau.

6. Progressively Growing of GANs for Improved Quality, Stability, and Variation — Karras et al (2017)

   Đây là một bài báo phải đọc vì các kết quả ấn tượng và cách tiếp cận sáng tạo cho lớp bài toán GAN. Bài báo này sử dụng kiến trúc multi-scale trong đó GAN xây dựng các layer có kích thước từ \(4\times 4\) cho đến \(1024\times 1024\). Sự không ổn định của GAN bị gia tăng phần lớn do kích thước của độ phân giải hình ảnh mục tiêu (target image resolution size), bài báo đã chỉ ra một cách giải quyết cho vấn đề này.

7. StackGAN — Zhang et al. (2017)

   StackGAN thực sự độc đáo và khác biệt so với các chủ đề trước ở trong danh sách này. Mô hình này tương tự Conditional GANs và Progressively Growing GANs. Đối với Progressively Growing GANs, StackGAN làm việc giống theo nghĩa nó tương tác trên nhiều tỉ lệ (multiple scales). Đầu tiên, mô hình này outputs ra một bức ảnh \(64\times 64\) và sau đó nó sử dụng thông tin này như là thông tin biết trước (prior information) để sinh ra một bức ảnh có độ phân giải \(256\times 256\). StackGAN đặc biệt bởi vì nó có thể sinh ra ảnh từ văn bản (natural language text to image). Bài báo này rất thú vị để đọc và nó trở nên tuyệt vời khi thấy được sự kết hợp giữa việc kiểm soát được latent space (không gian ẩn) trong StyleGAN với giao diện ngôn ngữ tự nhiên được định nghĩa trong StackGAN. Đây là mô phỏng kiến trúc mô hình.

8. CycleGAN — Zhu et al. (2018)

   CycleGAN tập trung vào bài toán image-to-image hơn là tổng hợp ảnh từ một véc tơ ngẫu nhiên. CycleGAN đặc biệt hơn khi xử lí chuyển đổi image-to-image khi chúng ta không có trong tay các cặp training samples (dữ liệu, nhãn). Bài báo này đề cập đến việc xây dựng hàm mất mát Cycle-Consistency và trực giác về cách huấn luyện GAN trở nên ổn định. Có nhiều ứng dụng hay được sử dụng với CycleGAN, như là super-resolution, style transfer, horse to zebra.

9. BigGAN — Brock et al (2019)

   Đây là một trong những state of the art trên ImageNet. Mô hình này rất khó để triển khai trên máy cá nhân (local machine), nó có nhiều các thành phần kiến trúc như Self-Attention, Spectral Normalization, và cGAN (Conditional GAN) với phép chiếu các thành phần phân biệt (projection discriminators), được giải thích kỹ trong bài báo. Tuy nhiên, bài báo này cung cấp một cái nhìn tổng thể tuyệt vời cho các ý tưởng của các bài báo nền tảng, hợp thành state of the art như hiện tại.

10. StyleGAN — Karras et al (2019)

    Đây là một mô hình thú vị, đặc biệt đối với lớp bài toán Latent Space Control. Mô hình này mượn cơ chế từ Neural Style Transfer, được biết tới với tên gọi Adaptive Instance Normalization, hay AdaIN, để kiểm soát không gian véc tơ ẩn theo cách khác với những nghiên cứu trước đây. Sự kết hợp giữa mapping network và phân phối AdaIN thông qua mô hình generator làm cho StyleGAN thực sự khá là khó để xây dựng, nhưng mô hình này rất hay và chứa đựng nhiều ý tưởng thú vị.

Bạn có thể xem video tóm tắt các cột mốc này.

Đi sâu vào khám phá GAN

Ở phần này, tôi sẽ chỉ tập trung khám phá GAN nguyên thủy, tức là GAN trong bài báo đầu tiên của Ian Goodfellow. Khi có thời gian, tôi sẽ tiếp tục viết về các mô hình khác trong hệ sinh thái GANs với những cấu trúc toán học trong đó.

Ý tưởng quan trong nhất trong GAN liên quan đến một định lý nổi tiếng, của một nhà toán học có ảnh hưởng lớn trong thế kỷ trước: John Nash, ông là nhà toán học duy nhất từ trước đến nay được trao giải Nobel về kinh tế.

Nếu có thời gian, tôi khuyến khích bạn nên coi phim này: A beautiful mind, đây là một bộ phim tiểu sử năm 2001 của Mỹ kể về cuộc đời của ông. Bộ phim được đạo diễn bởi Ron Howard và biên kịch là Akiva Goldsman. Cảm hứng làm phim được lấy từ một cuốn sách cùng tên rất nổi tiếng của nhà văn Sylvia Nasar, người từng được đề cử Giải Pulitzer năm 1988.

Minimax game

Lưu ý: Phần đầu sẽ trình bày qua ví dụ để hiểu về Minimax, phần sau sẽ đi sâu vào các chứng minh thuần túy.

Ngay từ phần abstract, tác giải đã đề cập đến mô hình GAN như là một trò chơi Minimax giữa hai người chơi, vậy Minimax là trò chơi như thế nào?

Trong lí thuyết trò chơi (game theory), Minimax (có khi gọi là MinMax, MM, hoặc saddle point) là giá trị nhỏ nhất mà những người chơi khác có thể buộc người chơi nhận được, mà không biết hành động của người chơi; tương tự, đó là giá trị lớn nhất mà người chơi có thể chắc chắn nhận được khi họ biết hành động của những người chơi khác.

Giả sử người chơi \(i\) chọn chiến lược \(s_i\) và những người còn lại chọn chiến lược \(s_{-i}\). Ký hiệu \(v_i(s)\) là hàm lợi ích của người chơi \(i\) trong chiến lược \(s\), Minimax của trò chơi được định nghĩa \[ \overline{v_{i}}=\min_{s_{-i}} \max_{s_{i}} v_{i}\left(s_{i}, s_{-i}\right) \]

Ở đây:

• \(i\) là chỉ số của người chơi quan tâm.
• \(-i\) biểu thị tất cả những người chơi còn lại (trừ \(i\)).
• \(s_i\) (\(s\) là viết tắt của strategy, biểu thị chiến lược của người chơi \(i\).
• \(s_{-i}\) biểu thị chiến lược của những người chơi khác.
• \(v_i\) (\(v\) là viết tắt của value) là hàm giá trị của người chơi \(i\).

Một cách tương tự, Maximin là giá trị cao nhất mà người chơi có thể chắc chắn để có được mà không biết những hành động của người chơi khác; tương tự, đó là giá trị thấp nhất mà người chơi khác có thể buộc người chơi nhận khi họ biết hành động của người chơi. \[ \underline{v_{i}}=\max_{s_{i}} \min_{s_{-i}} v_{i}\left(s_{i}, s_{-i} \right)
\]

Ví dụ, bảng sau thể hiện các giá trị chi trả (payoff) của người chơi \(1\) (hàng) và người chơi \(2\) (cột) sau khi ra quyết định, đơn vị: đồng.

	1	2	3
1	-1	-2	-1
2	2	2	1
3	-1	-1	0

Ở đây, để đơn giản trong việc trình bày, ta đã ghi tắt, các giá trị trên bảng tính theo người chơi \(1\):

• Ví dụ, tại vị trí \(\left(0,0\right)\), giá trị \(-1\) tức là người chơi \(1\) phải trả 1 đồng cho người chơi \(2\), nếu ghi đầy đủ sẽ là \(-1,1\), thể hiện thêm nội dung người chơi \(2\) được nhận \(1\) đồng từ người chơi \(1\), nhưng như vậy là thừa, vì mọi thứ chỉ xảy ra với \(2\) người chơi.

Với người chơi \(1\):

• Maximin là giá trị lớn nhất của tập \(\left\lbrace -2, 1, -1\right\rbrace\), do đó bằng \(1\).
• Minimax là giá trị nhỏ nhất của tập \(\left\lbrace 2, 2, 1\right\rbrace\), do đó bằng \(1\).

Với người chơi \(2\):

• Maximin là giá trị lớn nhất của tập \(\left\lbrace -1, -2, -1\right\rbrace\), do đó bằng \(-1\).
• Minimax là giá trị nhỏ nhất của tập \(\left\lbrace -1, 2, 0\right\rbrace\), do đó bằng \(-1\).

Ta thừa nhận định lý sau

Với các giải thiết nêu trên, ta có \[ \underline{u_{i}} \leq \overline{u_{i}} \]

Theo trực giác, trong Maximin, tối đa hóa đến trước khi tối thiểu hóa, vì vậy người chơi \(i\) cố gắng tối đa hóa giá trị của họ trước khi biết những người khác sẽ làm gì; trong Minimax, tối đa hóa đến sau khi tối thiểu hóa, vì vậy người chơi \(i\) ở vị trí tốt hơn rất nhiều, họ tối đa hóa giá trị của họ khi biết những gì người khác đã làm.

Trong ví dụ trên, Maximin và Minimax bằng nhau. Trong trường hợp như vậy (không phải lúc nào cũng xảy ra!), chiến lược minimax cho hai người chơi sẽ mang lại cân bằng Nash (hay Nash Equilibrium) của trò chơi. Để hiểu về cân bằng Nash, tôi khuyến khích bạn hai tài liệu sau: TL1, TL2.

Trong zeros-sum games, cân bằng Nash luôn xảy ra khi Minimax và Maximin bằng nhau, hay \[\min _{x} \max _{y} f(x, y)=\max _{y} \min _{x} f(x, y).\]

Ứng dụng của Minimax cho zeros-sum games là đặc biệt quan trọng.

Trong zeros-sum games với hữu hạn các chiến lược, tồn tại một mức chi trả \(P\) và một chiến lược hỗn hợp (mixed strategy) với mỗi người chơi thỏa mãn

1. Người chơi \(1\) có thể nhận một mức chi trả tối đa \(P\), bất chấp chiến lược của người chơi \(2\).
2. Người chơi \(2\) có thể nhận một mức chi trả tối đa \(-P\), bất chấp chiến lược của người chơi \(1\). Định lý này tương đương với việc thiết lập trạng thái cân bằng Nash.

Chú ý rằng chiến lược Minimax có thể bị trộn lẫn, về mặt tổng quát

Chiến lược Minimax thuần túy cho mỗi người chơi không nhất thiết dẫn đến cân bằng Nash.

Ví dụ, xét bảng chi trả của hai người chơi (player \(A\): hàng, player \(B\) : cột) như sau

	1	2	3
1	3	-2	-2
2	-1	0	4
3	-4	-3	1

Rõ ràng lựa chọn Minimax cho người chơi \(A\) là chiến lược \(2\) (vì rủi ro nhất chỉ phải trả \(1\), trong khi chiến lược \(1\) rất có thể phải trả \(2\), chiến lược \(3\) rất có thể phải trả \(4\)). Tương tự, Minimax cho người chơi \(B\) cũng là chiến lược \(2\). Tuy vậy, nếu \(B\) tin rằng \(A\) sẽ chọn chiến lược \(2\) thì \(B\) sẽ chọn chiến lược \(1\) để được \(1\); sau đó \(A\) lại counter \(B\) bằng cách chọn chiến lược \(1\) để được \(3\); và sau đó \(B\) sẽ lại counter bằng cách chọn chiến lược \(2\); và cuối cùng cả hai người chơi sẽ nhận ra sự khó khăn khi đưa ra lựa chọn (cân bằng Nash không xảy ra). Vì vậy, một chiến lược ổn định hơn là cần thiết.

Một trong hai người chơi có thể thay đổi chiến lược của họ khi đã biết trước chiến lược của người chơi khác, một chiến lược hỗn hợp có thể được xây dựng như sau

• \(A\) không quan tâm đến chiến lược \(3\) vì có khả năng sẽ phải bạo trả đến \(4\) cho \(B\), \(B\) cũng chắc chắn không bao giờ chọn chiến lược \(3\) vì nó hoàn toàn bất lợi cho \(B\).
• Giả sử xác suất \(A\) chọn chiến lược \(1\) là \(a\) và xác suất chọn chiến lược \(2\) là \((1-a)\). Nếu \(B\) chọn chiến lược \(1\), kỳ vọng của \(A\) là \[3\times a-1\times(1-a) = 4a-1.\] Nếu \(B\) chọn chiến lược \(2\), kỳ vọng của \(A\) là \[-2\times a + 0\times(1-a) = -2a.\] Như vậy, để tránh việc phải trả cho \(B\) nhiều hơn \(\dfrac{1}{3}\), hai kỳ vọng này nên bằng nhau, khi đó \(a=\dfrac{1}{6}\).
• Tương tự, \(B\) có thể đảm bảo chắc chắn sẽ nhận được ít nhất là \(\dfrac{1}{3}\) mà không quan tâm \(A\) chọn gì, bằng cách chọn ngẫu nhiên chiến lược \(1\) với xác suất \(\dfrac{1}{3}\), và chọn ngẫu nhiên chiến lược \(2\) với xác suất \(\dfrac{2}{3}\).
• Với cách chọn như vậy, các chiến lược hỗn hợp giờ đây đã ổn định (stable), hệ lúc này là một cân bằng Nash.

Định lý Minimax có rất nhiều cách phát biểu, đây cũng là một trong những bài toán được nghiên cứu rất nhiều, một trong những phát biểu về định lý mà tôi tìm thấy trên wiki là

Cho \(X\) là lồi compact trong \(\mathbb{R}^n\) và \(Y\) là lồi compact trong \(\mathbb{R}^m\), cho hàm \(f: X\times Y\rightarrow \mathbb{R}\) là hàm liên tục có dạng lõm-lồi, tức là

• \(f(\cdot, y): X \rightarrow \mathbb{R}\) là lõm khi cố định \(y\).
• \(f(x, \cdot): Y\rightarrow \mathbb{R}\) là lồi khi cố định \(x\). Khi đó ta có \[\max_{x} \min_{y} f(x, y)=\max_{y} \min_{x} f(x, y).\]

Để có một cái nhìn khái quát hơn về Minimax, bạn có thể tìm hiểu thêm ở một tài liệu tổng hợp các phát biểu và chứng minh của lớp bài toán này (từ năm 1928 đến khoảng đầu những năm 2000), rất cụ thể tại đây.

Bây giờ, tôi sẽ chỉ trình bày định lý Minimax theo Von Neumman, một cách độc lập với tài liệu trên.

Minimax theo Von Neumman

Cho \(A\) là ma trận \(m\times n\) đại diện cho ma trận chi trả (payoff) của hai người chơi trong zeros-sum game. Khi đó, trò chơi tồn tại một giá trị và một cặp chiến lược hỗn hợp tối ưu cho hai người chơi.

Ở đây, cặp chiến lược hỗn hợp \((x,y)=((x_1,x_2,\ldots,x_m), (y_1,y_2.\ldots,y_n))\) với \(x, y\) là các véc tơ xác suất tương ứng cho mỗi người chơi khi ra quyết định.

Với một cặp chiến lược hỗn hợp \((x,y)\), ta định nghĩa \[V(x, y):=\sum_{i=1}^{m} \sum_{j=1}^{n} x_{i} a_{i, j} y_{j},\] trong đó \(a_{i,j}\) là payoff tại vị trí \((i,j)\) trong \(A\).

Một cặp chiến lược hỗn hợp \(\left(x^{\star}, y^{\star}\right)\) được gọi là một điểm cân bằng (hoặc cặp cân bằng), tiếng anh là equilibrium point (hoặc equilibrium pair) cho một trò chơi zero-sum hai người thỏa mãn \[ V\left(x, y^{\star}\right) \leq V\left(x^{\star}, y^{\star}\right) \text { với mọi } x \in X_{m}, \text { và } V\left(x^{\star}, y^{\star}\right) \leq V\left(x^{\star}, y\right) \text { với mọi } y \in Y_{n}. \] Điều này tương đương với \[\max_{x \in X_{m}} V\left(x, y^{\star}\right)=V\left(x^{\star}, y^{\star}\right)=\min_{y \in Y_{n}} V\left(x^{\star}, y\right).\]

Ta có định lý sau

Các mệnh đề sau là tương đương

1. Tồn tại một cặp cân bằng.
2. \(v_{A}:=\max_{x \in X_{m}} \min_{y \in Y_{n}} V(x, y)=\min_{y \in Y_{n}} \max_{x \in X_{m}} V(x, y):=v_{B}\).
3. Tồn tại \(\mathbf{v} \in \mathbb{R}\) và \(x^{(o)} \in X_{m}, y^{(o)} \in Y_{n}\) sao cho
   a) \(\sum_{i=1}^{m} a_{i, j} x_{i}^{(o)} \geq \mathbf{v}, \quad j=1,2, \ldots, n\).
   b) \(\sum_{j=1}^{n} a_{i, j} y_{j}^{(o)} \leq \mathbf{v}, \quad i=1,2, \ldots, m\).

Chứng minh

\((1)\Rightarrow (2)\): Xét cặp cân bằng \(\left(x^{\star}, y^{\star}\right)\), ta có

\[\begin{eqnarray} v_{B} &=&\min_{y \in Y_{n}} \max_{x \in X_{m}} V(x, y) \leq \max_{x \in X_{m}} V\left(x, y^{\star}\right)=V\left(x^{\star}, y^{\star}\right) \\ &=&\min_{y \in Y_{n}} V\left(x^{\star}, y\right) \leq \max_{x \in X_{m}} \min_{y \in Y_{n}} V(x, y)=v_{A} \end{eqnarray}\]

\(v_A \le v_B\) là hiển nhiên, vậy nên đẳng thức xảy ra.

\((2)\Rightarrow (3)\): Giả sử rằng \(\mathbf{v} = v_A = v_B\). Ký hiệu \(x^{(o)}\) là vec tơ Maximin và \(y^{(o)}\) là véc tơ Minimax.

Khi đó với mọi \(j=1,2, \ldots, n\) và \(i=1,2, \ldots, m\) ta luôn có \(\begin{eqnarray} \sum_{i=1}^{m} a_{i, j} x_{i}^{(o)} &=& V\left(x^{(o)}, \beta_{j}\right) \geq \min_{y \in Y_{n}} V\left(x^{(o)}, y\right)=\max_{x \in X_{m}} \min_{y \in Y_{n}} V(x, y) \\ &=&\mathbf{v}=\min_{y \in Y_{n}} \max_{x \in X_{m}} V(x, y)=\max_{x \in X_{m}} V\left(x, y^{(o)}\right) \\ & \geq & V\left(\alpha_{i}, y^{(o)}\right)=\sum_{j=1}^{n} a_{i, j} y_{j}^{(o)}. \end{eqnarray}\)

\((3)\Rightarrow (1)\): Từ \(a)\) và \(b)\) ta suy ra \[ V\left(x^{(o)}, y\right) \geq \mathbf{v} \geq V\left(x, y^{(o)}\right) \text { với mọi } x \in X_{m} \text { và } y \in Y_{n}. \] Đặt \(x=x^{(o)}\) và \(y=y^{(o)}\) trong bất đẳng thức trên, ta thấy \(\mathbf{v}=V\left(x^{(o)}, y^{(o)}\right)\) và do vậy \(\left(x^{(o)}, y^{(o)}\right)\) là một cặp cân bằng.

Ta nhắc lại mà không chứng minh định lý của Brouwer

Cho \(K \subset \mathbb{R}^{p}\) là tập lồi, đóng, bị chặn. Khi đó nếu \(f: K \longrightarrow K\) liên tục thì tồn tại một \(\hat{x} \in K\) sao cho \(f(\hat{x})=\hat{x}\). (\(\hat{x}\) được gọi là điểm cố định của hàm \(f\)).

Chứng minh định lý của Von Neumman như sau

Chứng minh

Ta biết rằng tập \(X_{m} \times Y_{n}\) các cặp chiến lược hỗn hợp là đóng, bị chặn và lồi trong \(\mathbb{R}^{m+n}\). Ta định nghĩa một hàm chuyển (transformation) \(T: X_{m} \times Y_{n} \longrightarrow X_{m} \times Y_{n}\). Đặt

\[\begin{eqnarray} c_{i}(x, y) &:=& V\left(\alpha_{i}, y\right)-V(x, y) \text { (nếu đại lượng này dương) } \\ &:=& 0, \text {ngược lại} \end{eqnarray}\] \[\begin{eqnarray} d_{j}(x, y)&:=& V(x, y)-V\left(x, \beta_{j}\right) & \text { nếu đại lượng này dương} \\ & := & 0, \text { otherwise } \end{eqnarray}\]

Với mỗi \((x, y) \in X_{m} \times Y_{n}\), ta định nghĩa \(T(x, y)=\left(x^{\prime}, y^{\prime}\right)\) bởi \[x_{i}^{\prime}:=\frac{x_{i}+c_{i}(x, y)}{1+\sum_{k=1}^{m} c_{k}(x, y)} \text { và } y_{j}^{\prime}:=\frac{y_{j}+d_{j}(x, y)}{1+\sum_{k=1}^{n} d_{k}(x, y)}\] Chú ý rằng \(x_{i}^{\prime} \geq 0\) vì \(x_i \ge 0, c_i \ge 0\) và \(1+\sum_{k} c_{k} \geq 0\). Hơn nữa ta có \[\sum_{i=1}^{m} x_{i}^{\prime}=\left(\frac{1}{1+\sum_{k=1}^{m} c_{k}(x, y)}\right) \sum_{i=1}^{m}\left(x_{i}+c_{i}(x, y)\right)=1\] Tương tự như vậy, \(y_{j}^{\prime} \geq 0\) và \(\sum_{j} y_{j}^{\prime}=1\). Do đó \(T\) ánh xạ \(X_{m} \times Y_{n}\)vào chính nó. Ngoài ra, dễ kiểm tra từ định nghĩa \(T\) là hàm liên tục.

Trước tiên ta chỉ ra rằng \((\hat{x}, \hat{y})\) là một cặp cân bằng nếu và chỉ nếu nó là điểm cố định cho ánh xạ \(T\).

\((\Rightarrow)\): Giả sử \((\hat{x}, \hat{y})\) là một cặp cân bằng. Từ định nghĩa suy ra ngay \(c_i(\hat{x}, \hat{y})=0\) với mọi \(i\), do vậy \(\hat{x_i}^{\prime}=\hat{x_i}\) với mọi \(i\). Tương tự \(\hat{y_j}^{\prime}=\hat{y_j}\) với mọi \(j\). Do đó \(T(\hat{x}, \hat{y}) = (\hat{x}, \hat{y})\).

\((\Leftarrow)\): Giả sử \((\hat{x}, \hat{y})\) là một điểm cố định của \(T\). Trước tiên ta sẽ chỉ ra rằng phải có ít nhất một chỉ số \(i_0\) để \(\hat{x_{i_0}}>0\) và \(c_i(\hat{x}, \hat{y})=0\).

Do \(\displaystyle V(\hat{x},\hat{y})=\sum\limits_{i=1}^m \hat{x_i} V(\alpha_i,\hat{y})\), ta có thể kết luận \(V(\hat{x},\hat{y}) < V(\alpha_i, \hat{y})\) không đúng với mọi \(i\) để \(\hat{x_i} > 0\). Suy ra tồn tại \(i_0\) sao cho \(c_{i_0}(\hat{x}, \hat{y}) = V(\alpha_{i_0}, \hat{y}) - V(\hat{x}, \hat{y}) = 0\). Nhưng khi đó, giả thiết \((\hat{x}, \hat{y})\) là điểm cố định của \(T\) suy ra \[ \displaystyle x_{i_0} = \dfrac{\hat{x_{i_0}}}{1+\sum\limits_{k=1}^m c_k (\hat{x}, \hat{y})}, \] do đó \(\sum_k c_k(\hat{x}, \hat{y})=0\), lại vì \(c_k(\hat{x}, \hat{y})\ge 0\) nên \(c_k(\hat{x}, \hat{y})=0, \forall k\).

Từ đó, chúng ta có thể kết luận rằng \((\hat{x},\hat{y})\) là một cặp cân bằng. Kết thúc chứng minh. \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\blacksquare\)

Cách mà GAN hoạt động

Trong khi tìm dữ liệu để viết bài này, tôi bắt gặp một video giải thích khá dễ hiểu về cơ chế hoạt động của GAN.

Ý tưởng cơ bản của GAN là thiết lập một trò chơi hai người. Một trong số đó là Generator, Generator tạo ra các samples từ latent space (không gian ngầm, ẩn) có cùng phân phối với dữ liệu huấn luyện. Người chơi còn lại là Discriminator, người này đánh giá các samples và xác định xem sample là thật hay giả.

Generator được huấn luyện để lừa Discriminator.

We can think of the generator as being like a counterfeiter, trying to make fake money, and the discriminator as being like police, trying to allow legitimate money and catch counterfeit money. To succeed in this game, the counterfeiter must learn to make money that is in-distinguishable from genuine money, and the generator network must learn to create samples that are drawn from the same distribution as the training data.

Ta có thể nghĩ rằng Generator giống như một kẻ làm tiền giả, cố gắng tạo tiền giả, và Discriminator giống như người cảnh sát, cố gắng cho phép tiền hợp pháp và bắt tiền giả. Để thành công trong trò chơi này, người làm giả phải học cách làm tiền giả không thể phân biệt với tiền thật và Generator phải học cách tạo các mẫu được trích ra từ cùng phân phối với dữ liệu đào tạo.

Một diễn giải ngây thơ cho ví dụ này như sau: Lúc đầu, những tờ tiền giả có thể dễ dàng phát hiện ra (do tay nghề của kẻ làm tiền giả chưa cao). Sau đó, kẻ lừa đảo này sẽ phát hiện và cải tiến công nghệ, từ đó nâng cao chất lượng của tiền giả (ngày càng giống với tiền thật). Song song với điều đó, viên cảnh sát cũng học được những chi tiết mà kẻ lừa đảo cố gắng để tạo ra tiền giả (màu tờ tiền, khung viền, chất liệu giấy in, mùi thơm tờ tiền,…) Từ đó anh ta càng ngày càng giỏi trong chuyên môn chống tội phạm in tiền giả. Cho đến khi cả hai không thể giỏi hơn được nữa: Những tờ tiền giả được làm tốt đến mức người cảnh sát kia không tài nào phân biệt được, và kẻ làm tiền giả cũng không có thể cải tiến thêm bất kỳ điều gì cho những tờ tiền giả của hắn (bởi vì nó quá hoàn hảo, hắn nghĩ và cười lớn). Khi mà những kẻ trong cuộc chơi này không thể phát triển thêm điều gì để nó thú vị hơn, cân bằng Nash xảy ra.

Kẻ lừa đảo lấy nguyên liệu từ đâu để làm tiền giả ?

Nguyên liệu để làm tiền giả chính là nhiễu (noise), kí hiệu là \(z\), trong đó \(z\) được lấy ngẫu nhiên từ một Latent space với phân phối cho trước nào đó, có thể là phân phối chuẩn, phân phối đều,…

Latent space

If I have to describe latent space in one sentence, it simply means a representation of compressed data.

Trong thống kê, latent variables (Các biến tiềm ẩn) là các biến không được quan sát trực tiếp nhưng được suy ra (thông qua mô hình toán học ) từ các biến khác được quan sát (đo trực tiếp).

Tôi không tìm được một định nghĩa chính quy của Latent space (không gian tiềm ẩn), tuy vậy tôi thấy một số định nghĩa sau có thể chấp nhận được, xin nêu ra để mọi người cùng tìm hiểu

• Latent space là không gian của các biến tiềm ẩn.
• Latent space đề cập đến một không gian đa chiều trừu tượng chứa các đặc trưng mà chúng ta không thể giải thích trực tiếp, nhưng mã hóa một biểu diễn bên trong có ý nghĩa của các sự kiện được quan sát bên ngoài. (Nguồn)
• Latent space đơn giản là một đại diện của dữ liệu bị nén (compressed data).

Một cách hiểu về Compressed data

Auto Encoder hoạt động thông qua việc: Encoder (bộ mã hóa) làm giảm kích thước dữ liệu qua các layer, đưa vào một bottleneck layer, sau đó Decoder (bộ giải mã) chuyển encoded input về lại kích thước ban đầu. Compressed data chính là data thuộc vào bottleneck layer.

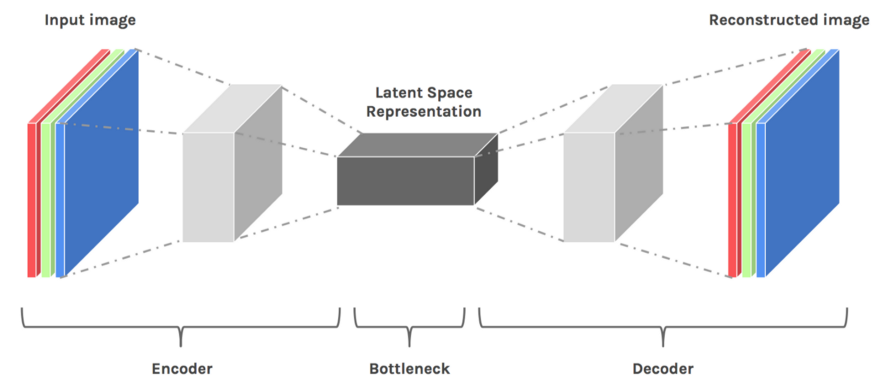
Ý tưởng của Latent space là quan trọng bởi vì nó là nhân tố chính của Deep Learning - học các đặc trưng của dữ liệu và đơn giản hóa các biểu diễn của dữ liệu cho mục đích tìm kiếm các mẫu.

Ví dụ như trong bài toán nhận dạng chữ số viết tay dữ liệu MNIST, ta phải huấn luyện để mô hình có thể nhận dạng được các chữ số khác nhau, cho dù chúng có thể có những đường nét khá giống nhau (chẳng hạn số \(3\) và số \(8\)). Trong lúc huấn luyện như vậy, ta đã làm cho mô hình học được những nét tương đồng trong cấu trúc giữa các ảnh với nhau, bằng cách tìm hiểu đặc trưng của mỗi chữ số (mỗi ảnh). Latent space có thể coi là một tập hợp các latent sample như hình dưới

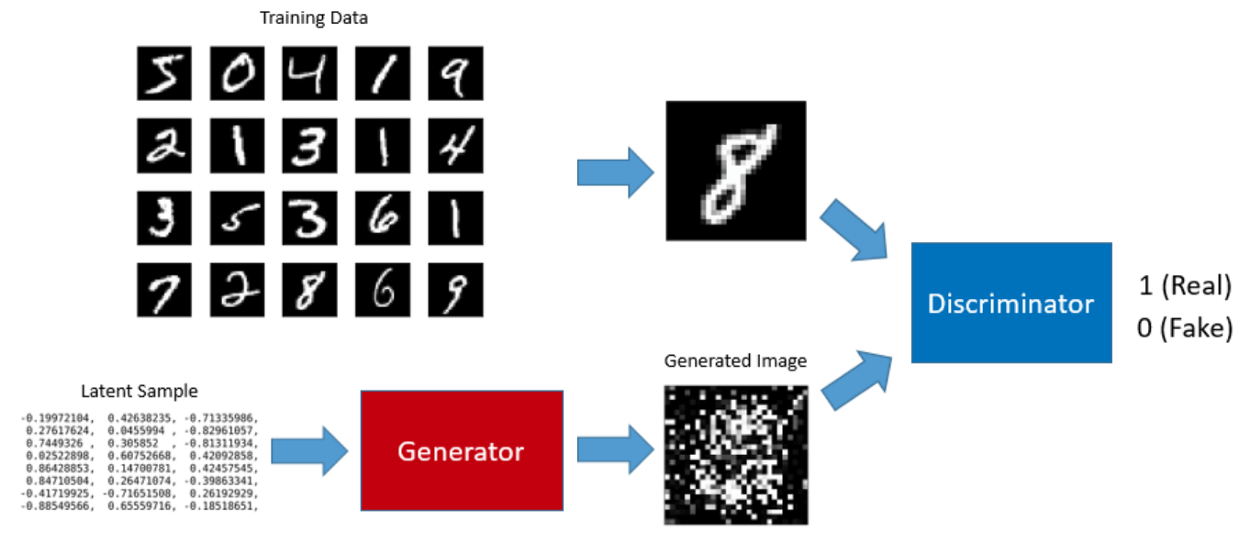
Kẻ lừa đảo (Generator) và Người cảnh sát (Discriminator)

Để hiểu cụ thể phần này, tôi khuyến khích bạn đọc kỹ hướng dẫn trong Deep Convolutional Generative Adversarial Network, một tutorial trong GAN của Tensorflow.

Hình dưới đây là sơ đồ cấu trúc hoạt động của GAN, để bạn có thể nắm được luồng di chuyển của data.

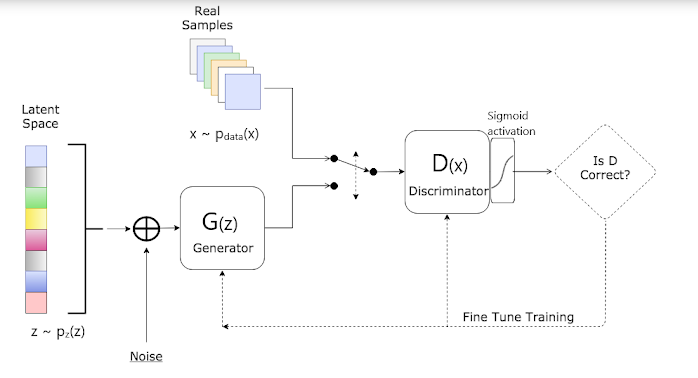
Về mặt ký hiệu

\[\begin{aligned} D: & \text{ Discriminator} \\ G: & \text{ Generator} \\ \theta_d: & \text{ Tham số của Discriminator} \\ \theta_g: & \text{ Tham số của Generator} \\ p_z(z) :& \text{ Phân phối của nhiễu (noise) đầu vào} \\ p_{data}(x): & \text{ Phân phối của dữ liệu gốc} \\ p_g(x): & \text{ Phân phối của Generator} \end{aligned}\]

Chiến lược: Tìm \(G\) để \(p_g(x) = p_{data}(x), \forall x\). Nếu nghiệm \(G\) tìm được thỏa mãn phương trình trên, ta có thể mong đợi rằng \(G\) là một mạng neural giúp chúng ra sinh ra những dữ liệu chân thật. Cùng nhìn một thành quả của GAN.

Generator (\(G)\) hay Discriminator \((D)\), bản chất cũng là các mạng neural với nhiều layer.

Generator nhận đầu vào là noise \(z\) để tạo thành fake data \(G(z)\), Discriminator nhận đầu vào là cả real data \(x\) lẫn fake data \(G(z)\).

Ngoài ra có thể hiểu về mặt toán học:

• \(G: \mathbb{Z}\longrightarrow \mathbb{Y}\) là một hàm khả vi (differentiable function) đi từ Latent space \(\mathbb{Z}\)vào \(\mathbb{Y}\), được đại diện bởi một multilayer perceptron với các tham số \(\theta_g\). (\(G\) phải cần đến điều kiện khả vi là để phục vụ quá trình cập nhật trọng số thông qua lan truyền ngược backpropagation. Khi có thời gian tôi sẽ viết kỹ về phần này).

• \(D:\mathbb{X}\cup\mathbb{Y}\longrightarrow [0,1]\) là một hàm xác suất đi từ không gian \(\mathbb{Y}\) hoặc không gian dữ liệu thật \(\mathbb{X}\), đại diện bởi một multilayer perceptron với các tham số \(\theta_d\). \(D(x)\) biểu diễn một xác suất thể hiện \(x\) đến từ dữ liệu thật chứ không phải từ \(p_g\).

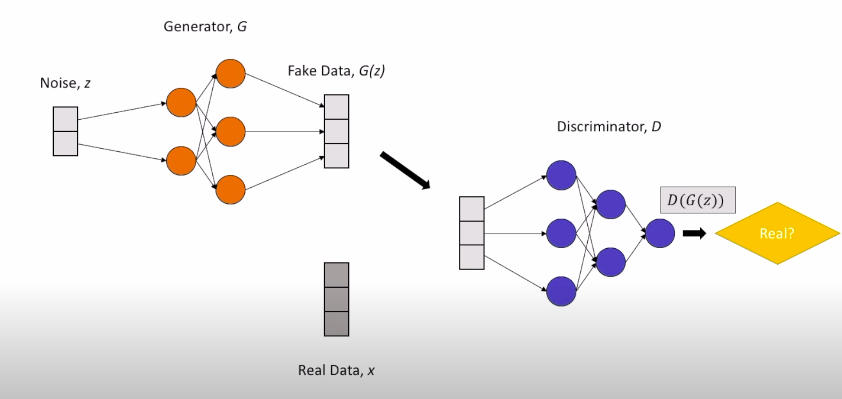
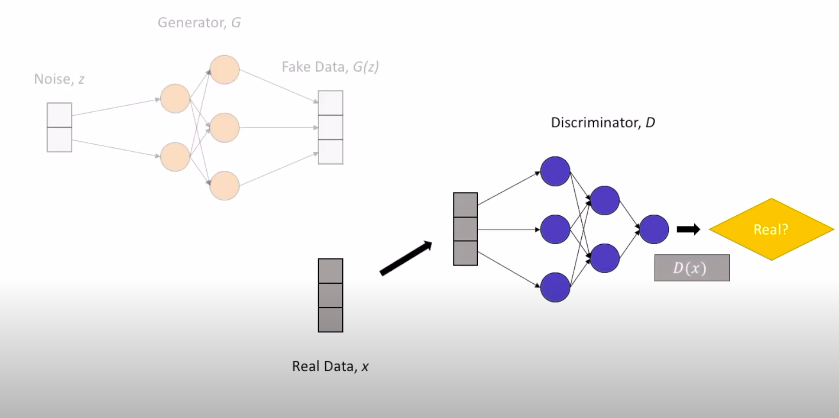
Bạn có thắc mắc tại sao \(G\) và \(D\) lại nhận đầu vào như vậy không ?

Câu trả lời rất đơn giản, bởi vì việc của \(G\) là sinh ra fake data, nên \(G\) đương nhiên cần nguồn nguyên liệu fake, tức là noise \(z\). Còn \(D\) có nhiệm vụ phân biệt real data và fake data, nên \(D\) phải cần đủ cả hai dữ liệu real (\(x\)) và \(G(z)\) (fake data), bởi lẽ không ai có thể nhận biết thật giả nếu không được quan sát chúng, đúng chứ ?

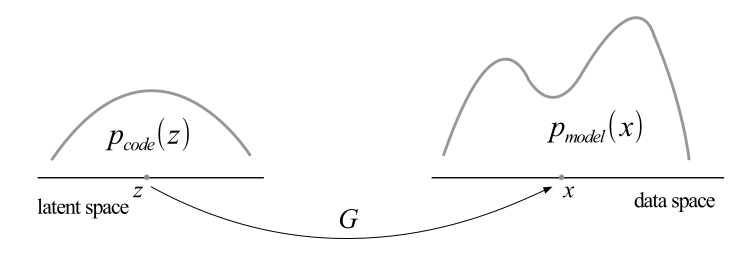
Khi ta huấn luyện \(G\) thành công, \(G\) sẽ là một transformation như hình dưới đây.

Các hàm mất mát (loss function)

Chúng ta huấn luyện \(D\) để maximize xác suất gán nhãn đúng cho cả mẫu huấn luyện và mẫu đến từ \(G\). Song song đó, ta cũng huấn luyện \(G\) để minimize \(\log(1-D(G(z))\).

Nói một cách khác, \(G\) và \(D\) đang chơi một trò chơi minimax dành cho hai người với hàm giá trị \(V(G,D)\), đây cũng chính là loss function trong GAN.

\[ \displaystyle \min_{G} \max_{D} V(G,D) = \mathbb{E}_ {x \sim p_{data}(x) } [\log D(x)] + \mathbb{E}_ {z\sim p_{z}(z)}[\log (1-D(G(z)))]. \] Để hiểu kỹ công thức về phía bên phải dấu bằng, tôi khuyến khích bạn xem phần Về cross-entropy trong Machine Learning, trong bài Entropy Trong Lý Thuyết Thông Tin.

Rõ ràng mục tiêu của Discriminator là maximize giá trị \(D(x)\) đối với những điểm dữ liệu \(x\sim p_{data}(x)\) và minimize \(D(G(z))\) đối với những điểm dữ liệu \(z\sim p_z(z)\), tức là maximize \(1-D(G(z))\). Để ý rằng \(\max U\Leftrightarrow \max \log U, \forall 0< U \le 1\). Do vậy, mục tiêu của \(D\) là maximize tổng \[\mathbb{E}_ {x \sim p_{data}(x) } [\log D(x)] + \mathbb{E}_ {z\sim p_{z}(z)}[\log (1-D(G(z)))] = V(G,D).\]

Ký hiệu \(D\) tối ưu là \(D^*_ {G}=\operatorname{argmax}_D V(G,D)\), với \(G\) cho trước.

Bây giờ, giả sử đã có \(D = D^* _{G}\), do mục tiêu của \(G\) và \(D\) là ngược nhau, ta tìm \(G\) để minimize \(V(G,D)\), lúc này \(G\) tối ưu được ký hiệu \[G^*= \operatorname{argmin}_G V(G, D^ * _ G).\]

Ta đi chứng minh bài toán tối ưu có nghiệm duy nhất \(G^*\) thỏa điều kiện \(p_g = p_{data}\).

Theo định lý Radon-Nikodym, ta có \(\begin{aligned} V(G, D) &=\int_x p_{\text {data }}(x) \log (D(x)) d x+\int_z p_z(z) \log (1-D(G(z))) d z \\\ &=\int_x p_{\text {data }}(x) \log (D(x))+p_g(x) \log (1-D(x)) d x \end{aligned}\)

Với mọi \((a,b)\in \mathbb{R}\setminus \left\lbrace (0,0)\right\rbrace\). Xét hàm số \(f(u) = a\log u + b\log (1-u)\), tìm maximum của \(f\) đơn giản bằng đạo hàm \[f^{\prime}(u)=0\Leftrightarrow \dfrac{a}{u}-\dfrac{b}{1-u}=0\Leftrightarrow u = \dfrac{a}{a+b}.\] Thay \(u\) vừa tìm được vào đạo hàm bậc \(2\) của \(f\): \[f^{\prime \prime}(u)=-\frac{a}{(a+b)^{2}}-\frac{b}{\left(1-\frac{a}{a+b}\right)^{2}}<0.\] Từ đó \(\dfrac{a}{a+b}\) là maximum của \(f\). Do vậy \(D(x)=\dfrac{p_{\text {data}}(x)}{p_{\text {data}}(x)+p_{g}(x)}\) là maximum của tích phân trên.

Từ đó suy ra \(D^*_ G = \dfrac{p_{\text {data}}}{p_{\text {data}}+p_{g}}\).

Trong bài báo, \(C(G)\) được nhắc đến là mục tiêu huấn luyện ảo (virtual training criterion), và được ký hiệu

\[\begin{aligned} C(G) &=\max_D V(G, D) \\\ &=\mathbb{E}_ {x \sim p_{data}} \left[\log D_G^* (x)\right]+\mathbb{E}_ {z \sim p_z}\left[\log \left(1-D_G^* (G(z))\right)\right] \\\ &=\mathbb{E}_ {x \sim p_{data}}\left[\log D_G^* (x)\right]+\mathbb{E}_ {x \sim p_g}\left[\log \left(1-D_G^*(x)\right)\right] \\\ &=\mathbb{E}_ {x \sim p_{data}} \left[\log \dfrac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]+\mathbb{E}_ {x \sim p_g}\left[\log \dfrac{p_g(x)}{p_{data}(x)+p_g(x)}\right] \end{aligned}\]

• Với các phân phối xác suất \(p, q\) được định nghĩa trên cùng một không gian xác suất \(\mathbb{X}\), Độ đo Kullback–Leibler divergence từ \(q\) vào \(p\) được định nghĩa \[\operatorname{KL}(p \| q)=\sum_{x \in \mathbb{X}} p(x) \log \left(\dfrac{p(x)}{q(x)}\right).\]
• Với \(m=\dfrac{p+q}{2}\) là một phân phối xác suất, ta định nghĩa độ đo Jensen–Shannon divergence \[\operatorname{JSD}(p \| q)=\dfrac{1}{2} \operatorname{KL}(p \| m)+\dfrac{1}{2} \operatorname{KL}(q \| m).\]
• Độ đo Kullback–Leibler divergence không phải là một mê tríc, do đó không có tính đối xứng: \(\operatorname{KL}(p \| q) \ne\operatorname{KL}(q \| p)\).
• Hai độ đo này đều không âm.
• Khi độ đo bằng \(0\), hiển nhiên \(p=q\).
• xem thêm về hai độ đo này ở 1 và 2.

Định lý quan trọng nhất của bài báo (Định lý 1)

Global minimum của \(C(G)\) đạt được khi và chỉ khi \(p_g = p_{data}\). Khi đó giá trị của \(C(G)\) là \(-\log 4\).

Chứng minh

Mục tiêu của GAN là \(p_{data} = p_g\), khi đó \(D^ * _G(x)= \dfrac{1}{2}\).

Nói vui: Lúc này Discriminator có đôi chút bối rối, giống như tâm trạng cô gái đến nhà bạn trai mà anh ta lại có một người anh em sinh đôi vậy, cô ấy không thể nhận ra ai mới là người yêu mình.

Lúc này \(C(G) = \log \dfrac{1}{2} + \log \dfrac{1}{2}=-\log 4\).

Mặt khác, ta biến đổi \(C(G)\) như sau \(\begin{aligned} C(G) &=\mathbb{E}_ {x \sim p_{data}} \left[(\log 2-\log 2)+\log \dfrac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]+\mathbb{E}_ {x \sim p_g}\left[(\log 2-\log 2)+\log \dfrac{p_g(x)}{p_{data}(x)+p_g(x)}\right]\\\ &=-2\log 2 + \mathbb{E}_ {x\sim p_{data}}\left[\log 2+\log \dfrac{p_{data}(x)}{p_g(x)+p_{data}(x)}\right] + \mathbb{E}_ {x\sim p_g}\left[\log 2+\log \dfrac{p_g(x)}{p_g(x)+p_{data}(x)}\right]\\\ &=-2\log 2 + \mathbb{E}_ {x\sim p_{data}}\left[\log \dfrac{p_{data}(x)}{(p_g(x)+p_{data}(x))/2}\right] + \mathbb{E}_ {x\sim p_g}\left[\log \dfrac{p_g(x)}{(p_g(x)+p_{data}(x))/2}\right] \end{aligned}\)

Theo Kullback–Leibler divergence, ta có \[C(G)=-\log 4+\operatorname{KL}\left(p_{data} \bigg\| \dfrac{p_{data}+p_{g}}{2}\right)+\operatorname{KL}\left(p_{g} \bigg\| \dfrac{p_{data}+p_{g}}{2}\right) = -\log 4+2 \cdot \operatorname{JSD}\left(p_{data} \| p_{g}\right)\ge -\log 4.\] Dấu bằng xảy ra khi và chỉ khi \(p_g = p_{data}\). Khi đó \(C^* = \min_G C(G) = -\log 4\). Suy ra \(p_g = p_{data}\) là nghiệm duy nhất để có được cân bằng Nash. \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\blacksquare\)

Thuật toán GAN

Mệnh đề về sự hội tụ trong GAN

Nếu \(G\) và \(D\) đủ năng lực cập nhật, và ở mỗi bước của thuật toán (I), Discriminator được tối ưu với \(G\) cho trước, và \(p_g\) được cập nhật để cải thiện C(G) thì \(p_g\longrightarrow p_{data}\).

Để phục vụ chứng minh mệnh đề trên, ta chứng minh bổ đề sau

Hàm dưới là lồi trong \(p_g\) \[U\left(p_{g}, D\right)=\mathbb{E}_ {x \sim p_{data}}[\log D(x)]+\mathbb{E}_ {x \sim p_{g}}[\log (1-D(x))].\]

Thật vậy, lấy \(x, y \in p_g\) và lấy \(\alpha\) bất kỳ trong \((0,1)\) thì

\(\mathbb{E}_{x,y\sim p_g} [\alpha\log(1-D(x))+(1-\alpha)\log(1-D(y))]=\alpha \mathbb{E}_{x\sim p_g}[\log(1-D(x))]+(1-\alpha)\mathbb{E}_{y\sim p_g}[\log(1-D(y))]\).

Từ đó \(U\left(p_{g}, D\right)\) lồi trên \(p_g\).

Bây giờ với tập chỉ số \(A\) và \(f_{a\in A}\) là hàm lồi trên \(p_g\). Ta đặt \(f(x)=\text{sup}_{a \in A} f_a (x), \forall x\in p_g\).

Lấy \(x_0\in p_g\), đặt \(b=\text{arg sup}_a f_a(x_0)\), suy ra \(f(x_0)=f_b(x_0)\).

Lấy \(v \in \partial f_b(x_0)\) (\(v\) là dưới gradient bất kỳ của \(f_b(x_0)\)). Từ định nghĩa của dưới gradient suy ra với \(y\) thuộc lân cận nhỏ tùy ý của \(x_0\), ta có \[f_b(y)\ge f_b(x_0) + \langle v, y-x_0 \rangle.\]

Từ \(f(y)=\text{sup}_a f_a(y)\ge f_b(y)\) suy ra \(f(y)\ge f(x_0)+ \langle v, y-x_0 \rangle\). Do đó \(v\in \partial f(x_0)\) nên \(\partial f_b(x_0) \subset \partial f(x_0)\).

Nếu \(f\) thêm điều kiện khả vi thì dưới gradient của \(f\) tại \(x\) cũng là gradient của \(f\) tại \(x\). Nói cách khác, dưới vi phân của supremum của một họ các hàm lồi tại một điểm luôn chứa gradient tại điểm mà hàm đó đạt cực đại.

Áp dụng điều này cho hàm lồi khả vi \(\text{sup}_D U(p_g, D)\).

Ta luôn có gradient để cập nhật cho \(G\) khi mà \(D\) được tối ưu. Do hàm lồi này chỉ có một cực trị toàn cục \(p_{data} = p_g\) như chứng minh ở định lý 1 nên khi cập nhật bằng Gradient Descent (thuật toán I), \(p_g\) sẽ dần hội tụ về \(p_{data}\).

Các hạn chế (Drawbacks) của GAN

Phần này tôi sẽ cập nhật sau.

Cảm ơn bạn đã đọc tới đây, tôi vẫn còn đang phải học hỏi nhiều nên rất mong nhận được ý kiến chia sẻ từ mọi người từ comments hoặc mails. Mến chào bạn.

Tài liệu tham khảo

[1]. Convergence Problems with Generative Adversarial Networks, S. A. Barnett.

[2]. Math behind gans, Mayank Vadsola Mayank Vadsola.

[3]. AI for comedy generative networks and latent spaces, Dirk Meulenbelt .

[4]. Latent space visualization deep learning, Julien Despois.

[5]. Understanding latent space in machine learning, Ekin Tiu.

[6]. DCGAN-Tensorflow